最大线段重合问题, TopK问题
最大线段重合问题
问题描述
给定很多线段,每个线段都有两个数 [start, end] ,表示线段开始位置和结束位置,左右都是闭区间规定:1)线段的开始和结束位置一定都是整数值;2)线段重合区域的长度必须>=1,也就是说仅顶点重合并不算重合区域。返回线段最多重合区域中,包含了几条线段。
问题分析
我们一步一步分析。
首先,怎么判断两条线段不重合?容易想到,当 line1.left >= line2.right 或 line1.right<=line2.left 时,就可以判定这两条线段不重合了。如下,line1.right<line2.left ,line3.left>line2.right 所以 line2 与 line1、line3 都不重合。
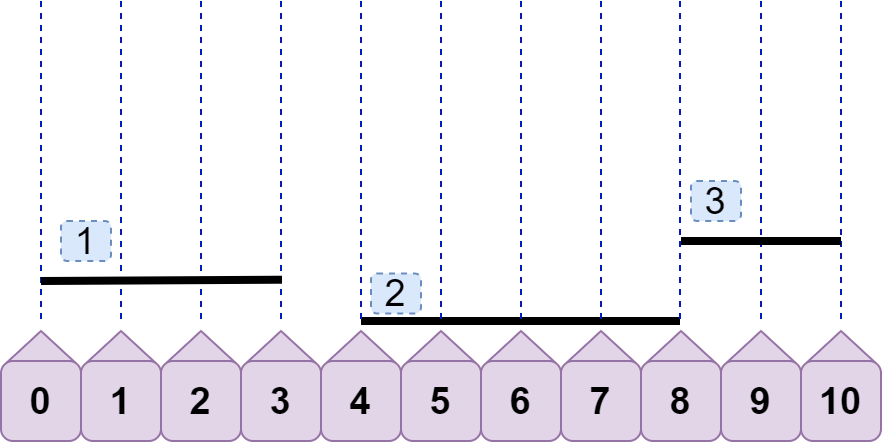
接着,如何判断两条线段不重合?仔细分析后可以发现,当 line1.left<=line2.left<line1.right 时,line1 与 line2 就发生重合(无需考虑 line2.right ),如下图:
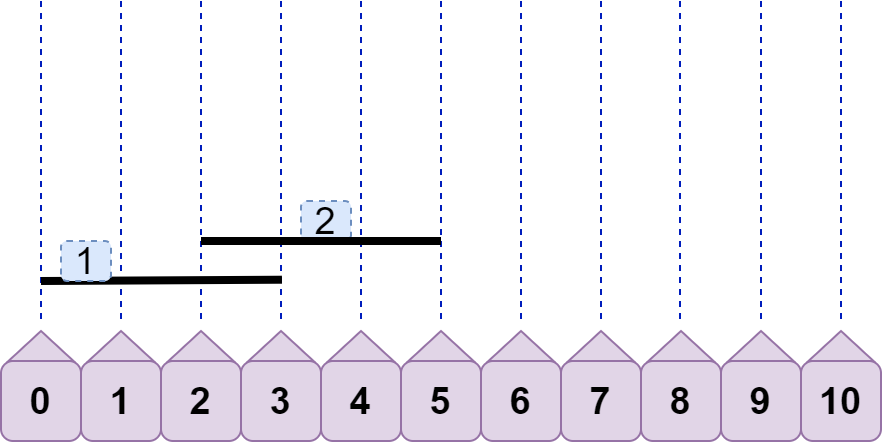
有读者一定会疑问,当 line2.left<=line1.left<line2.right 时,不也能重合吗? 注意,这种情况和上面的情况是相同的,只不过 line1 与 line2 互换了名字而已,这点很重要 。为了避免出现这两种情况的混淆,我们有必要先根据线段左端点的位置给所有线段排个序 ,如下图:
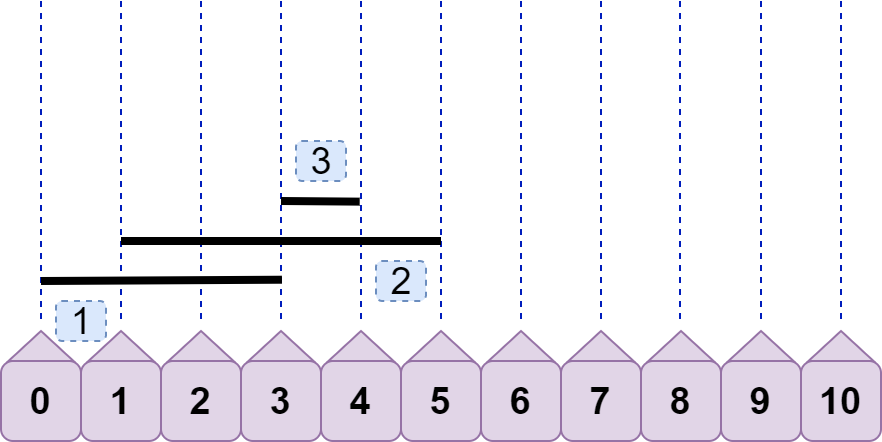
排好序后,我们判断是否重合时,就只需要考虑后面线段的左端点是否大于 前面线段的右端点(基准) ,即只用考虑 line2.left<line1.right ,因为排序后必有 line1.left<=line2.left 。
接着,我们来分析上图中的三条线段。line2.left<line1.right ,故 line2 与 line1 重合;line3.left=line1.right ,故 line3 与 line1 不重合;line3.left<line2.right ,故 line3 与 line2 重合,即现在有两种情况重合,且重合数都为 2。那么问题来了,我们该记录哪种情况的重合数呢?都记录?有必要吗?实际上,只需要记录 line2 与 line3 的重合数即可,这是因为后续加入的线段的左端点不可能小于 3(因为之前我们已经对所有线段完成了排序),所以后续线段不可能再与 line1 发生重合,故可以直接将 line1 丢弃(标记为绿色);如下图:
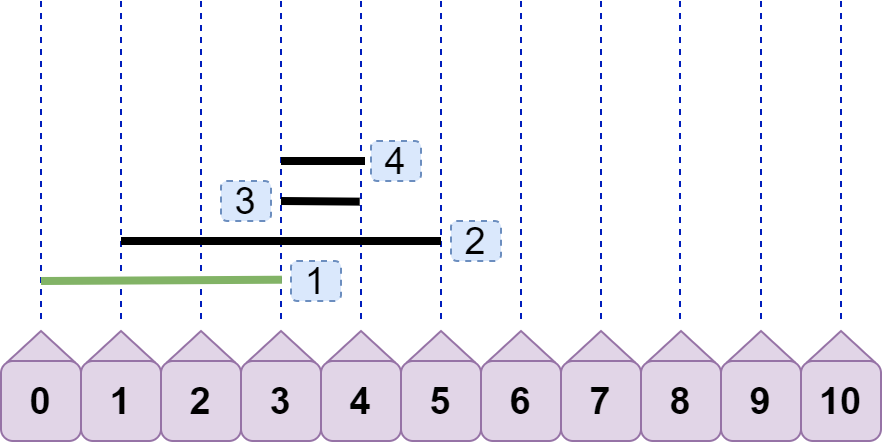
引入 line4,可见现在的最大重合数为 3,但这只是我们看出来的,还需要有一个固定的逻辑比较流程。如何得到最大重合数为 3?line4.left<line2.right 且 line4.left<line3.right ,所以得到重合数为 3?嗯,思路大致没错,聪明的你可能还会继续优化:只需要有 line4.left<line3.right 就可以直接得到 3,你给出的理由是:既然 line3.right<line2.right ,又因为 line4.left<line3.right ,所以一定有 line4.left<line2.right ,即不等式的传递性。果真是这样吗?那如果是下图情况呢:
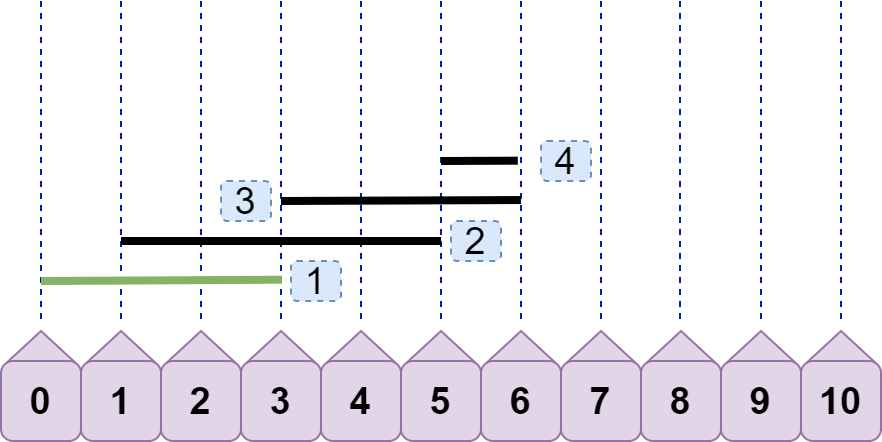
显然,line4.left<=line3.right ,重合数只有 2。但请注意,上图出现了我们之前讨论过的情况:后续线段左节点>=前面线段右节点,即line4.left>=line2.right 。按照之前的方案,我们将先 line2 丢弃:
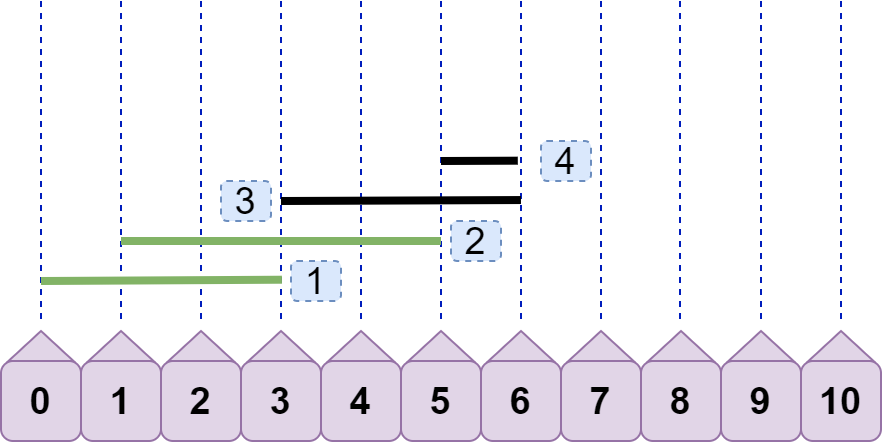
继续,由于 line4.left<line3.right ,所以得到重合数为 2。
由上分析,可知大致比较过程为:当加入新线段 lineN 时,依次丢弃之前的右端点小于等于 lineN.left 的线段,剩下的线段数即为最大重合数。
啊?不对呀?万一碰到下面情况:
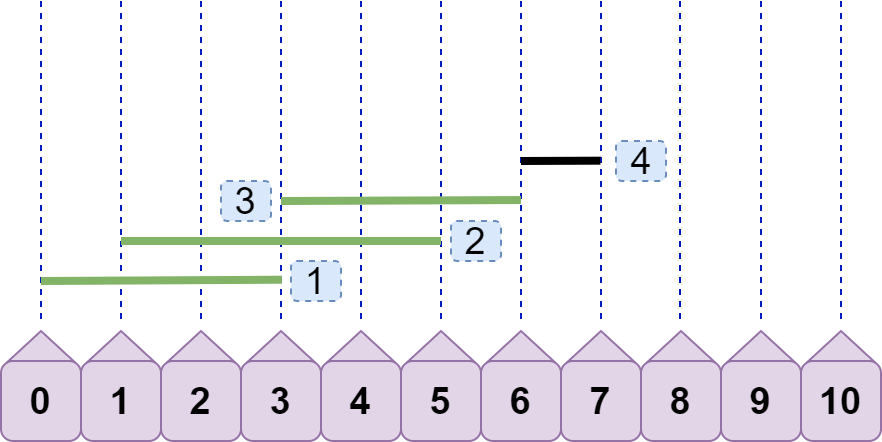
line4 将之前所有线段都弹出了,只剩 line4 一条线段了,但最大重合数不是 1,而是 2 呀!没错,所以我们还需要一个变量 max 来记录最大重合数,若当前重合数 cur>=max ,则 max=cur ;若 cur<max 则 max=max ,即 max=cur>max?cur:max; 。就上图而言,加入 line4 时,max=2;加入 line4 ,弹出之前的线段后,cur=1;cur<max,所以 max 仍然为 2。
下面给出全过程图示:
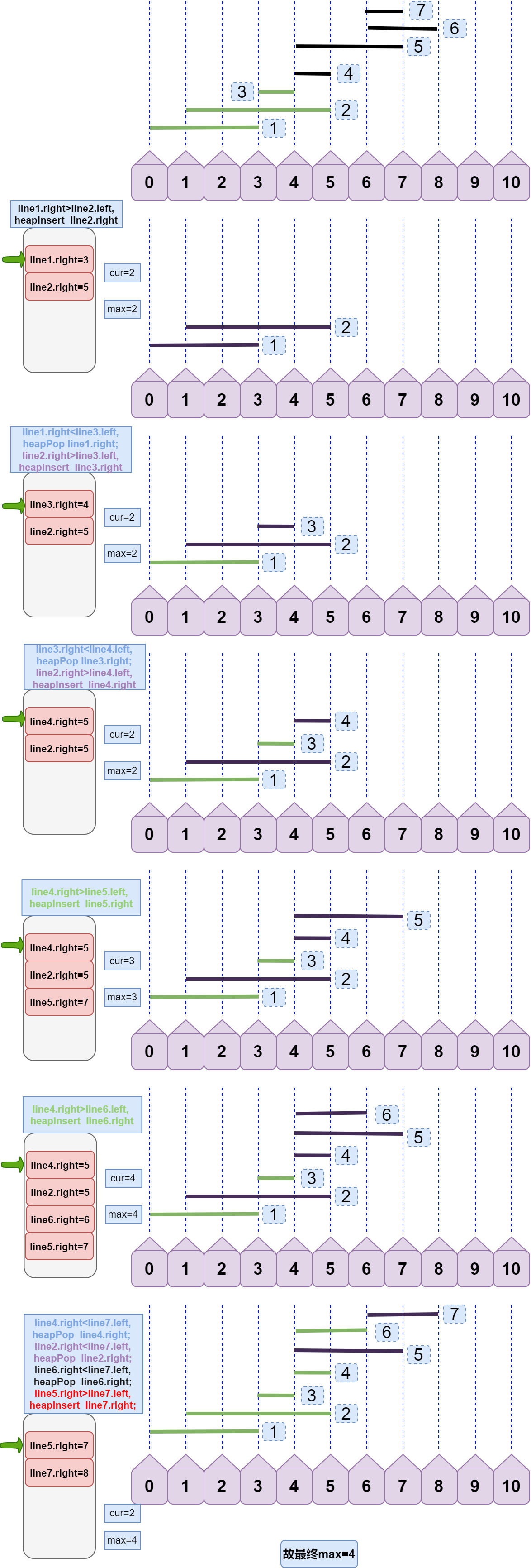
注意:左边灰色大框是堆结构,栈顶为堆中右端点最小的 right。
其实本算法中,堆结构并不关键,堆只是提供了取集合中最小值的便捷,难的还是其过程分析。
1 |
|
TopK问题
进行下面问题的探讨之前,请先移步《加强堆》 ,而后此问题将迎刃而解。
TopK实际应用
应用情形
某大型电商举办促销活动,从早上 8 点开始到晚上 12 点结束,这段时间内购买商品最多的前 K 位用户可以获得奖励,最终结果以 12 点的统计情况为准。为了提高用户参与活动的积极性,电商希望在平台官网实时更新并显示当前的得奖区用户(前K位用户)。排名具体规则如下:
1)得奖系统分为得奖区和候选区,任何用户只要购买数>0,一定在这两个区域中的一个;
2)某用户发生购买商品事件,购买商品数+1;发生退货事件,购买商品数-1;如果购买数不足以进入得奖区的用户,进入候选区;
3)每次都是最多 K 个用户得奖,K 也为传入的参数如果根据全部规则,得奖人数确实不够 K 个,那就以不够的情况输出结果;
4)如果某个用户购买商品数为 0,但是又发生了退货事件,则认为该事件无效,得奖、候选名单和上一个事件发生后一致;
5)购买数最大的前 K 名用户进入得奖区,在最初时如果得奖区没有到达 K 个用户,那么新来的用户直接进入得奖区;
6)当前事件发生的时间是指该操作对应的数组下标,比如下面代码中,5 对应的时间为其下标,即 6;
7)如果候选区购买数最多的用户,已经足以进入得奖区,该用户就会替换得奖区中购买数最少的用户( 大于才能替换 );如果得奖区中购买数最少的用户有多个,就替换最早进入得奖区的用户;如果候选区中购买数最多的用户有多个,机会会给最早进入候选区的用户;
8)从得奖区出来进入候选区的用户,进入候选区的时间就是当前事件的时间;从候选区出来进入得奖区的用户,进入得奖区的时间就是当前事件的时间;
其实上述规则虽然很多,但并不复杂,反而非常贴切实际生活,尤其是第 7、8 点,这些规则能够促使你不仅要买的多,也必须买的早。
1 | arr = [3 , 3 , 1 , 2, 1, 2, 5] |
以上代码中 arr[ ] 表示客户编号,op[ ] 表示客户操作;数组内容依次表示:3 用户购买了一件商品,3 用户购买了一件商品,1 用户购买了一件商品,2 用户购买了一件商品,1 用户退货了一件商品,2 用户购买了一件商品,5 用户退货了一件商品…
问题分析
注意字眼:“大型电商”——海量数据,“实时更新”——动态插入,“前K位”——优先级队列 。显然,这是一类海量数据+动态插入的优先级队列问题,首先考虑用堆来解决。容易想到,候选区与得奖区应该使用两个堆分别进行维护。又观察到同一个用户可以在多个时间段进行加购和退货操作,所以必须动态调整该用户在堆中的位置,所以考虑使用加强堆 。具体过程如下:
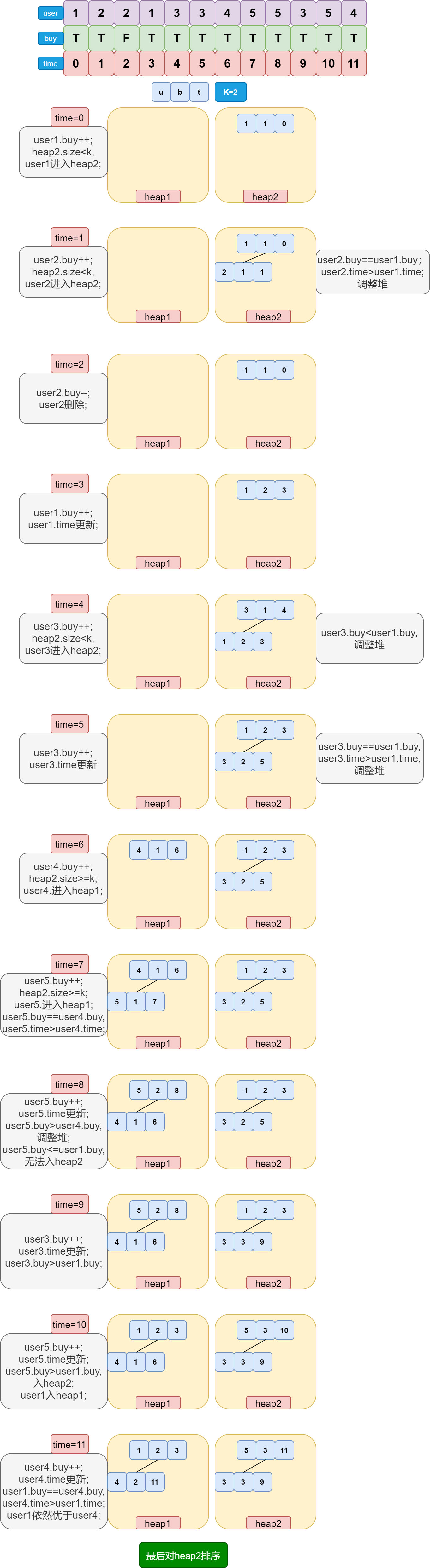
可别忘了规则中提到的几点:
- heap1是候选堆,heap2是得奖区。
- 候选区的堆顶是该堆中购买商品最多的用户,如果多个用户购买商品的数量相同,则时间点早的用户优先。得奖区的堆顶是该堆中购买商品最少的用户,如果多个用户购买商品的数量相同,则时间点早的用户优先。
- 当得奖区用户数没达到 K 时,新用户直接进入得奖区。
- 交换堆顶时,两个用户的时间点都会更新为当前的时间。
代码如下:
1 |
|
相关细节在注释中,除此外还需要强调:
- 开辟二维vector是为了减少判断哪个堆的代码量,比如在 heaplify() 和 heapInsert() 中,直接使用 hp 对某个堆进行操作,无需判断是哪个堆,减少了代码量。
- 比较器也在本算法中发挥了较大作用,减少了代码量,提高可读性,同时便于维护。关于比较器,详细参见:仿函数与比较器 。





