问题描述：
有 7 对数字:两个 1 ,两个 2 ,两个 3 ,…两个 7 ,把它们排成一行。要求,两个 1 间有 1 个其它数字,两个 2 间有 2 个其它数字,以此类推,两个 7 之间有 7 个其它数字。如下就是一个符合要求的排列:
1 7 1 2 6 4 2 5 3 7 4 6 3 5

请列出所有满足条件的排列。

问题分析：

稍作分析我们就可以得到以下结论：

  1. 放数字时，不仅要在当前位置放，还需要在关联位置上放：

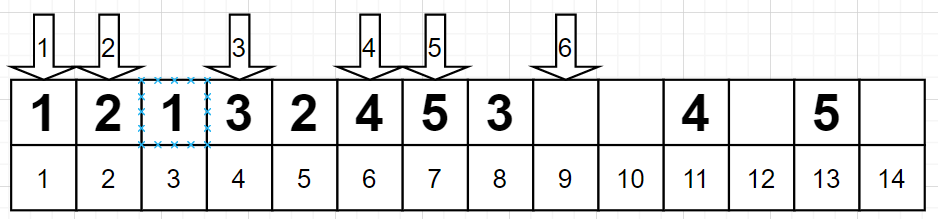    在 [4] 位置放置 3 时，也必须同时在 [8] 位置放置 3；

  2. 每放一个数字时，都需要将此数字标记为已放置。

  3. 放置数字时，必须在没有放置(未标记)的数字中 从小到大 试每个数字，直到能够放置或试完所有数字：

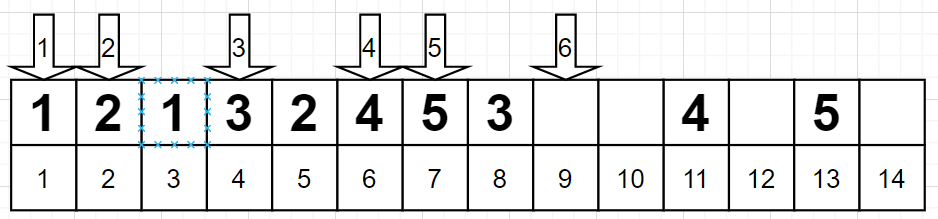
    在 [9] 位置放置时，遍历 1,2,3,4,5 发现都已标记，于是尝试 6，不可；在尝试 7，不可；于是撤销上一步操作；

  4. 当发现某个空白位不能放任何数字时，说明之前的放置方式是错误的， 需要撤回上一次的放置 ，并放置其他数字，再重复以上过程：
    在上图中，执行到第 6 步(箭头6)时陷入死路，于是撤回到第 5 步(箭头5)，并在此处尝试放置数字 6，可以：

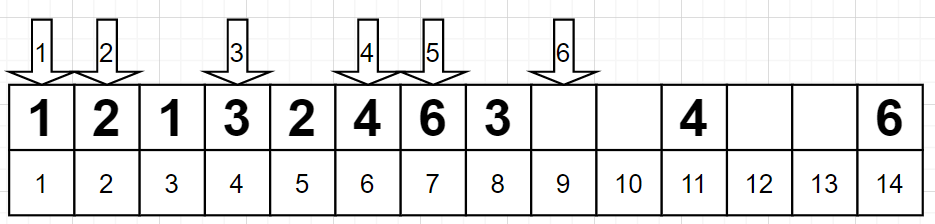
    然后在箭头 6 处放置数字；先考虑放置 5，不可；再考虑放置 7，不可；于是再次撤回到箭头 5，并在此放置数字 7，仍然不可；于是撤回到箭头 4，并在此处放置 5，可以：

    然后在箭头 5 处考虑放置数字 4，不可([12]被 5 占了)；考虑数字 6，可以，于是放置 6…

从以上过程可见，核心有两点：

  1. 从小到大依次放置数字
  2. 撤销操作的实现

实际上，这个过程可以抽象成如下动态变化的树：

执行到第 7 步时，只有数字 6 未标记，但无法放置，于是回退到第 6 步，之前放置的是数字 2，回退后就应该尝试放置数字 6，也无法放置；于是回退到第五步，之前放置的是数字 5，现在应该尝试放置数字 6，可以；重复以上步骤即可。下面给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<iostream>
using namespace std;
bool num[8] = { 0 };
int arr[15] = { 0 };
bool canPut(int i,int pos)
{
	if (!num[i] //是否被标记为已放
        && pos + 1 + i <= 14 && arr[pos + 1 + i] == 0)//该空白处是否能放
		return true;
	else
		return false;
}

void put(int k,int pos)//放置数字
{
	arr[pos] = k;
	arr[pos + 1 + k] = k;
	num[k] = 1;//标记该数字为已放true
}

void go(int pos, int n)
{
	if (pos>14)//判断所有数字是否已经put
	{
		for (int i = 1; i <= 14; i++)
			cout << arr[i] << " ";
		cout << endl;
		return;
	}
	
	if (arr[pos]!=0)//如果该位置有数字了，则再往前走一步
		go(pos + 1, n);
	else
		for (int k = 1; k <= 7; k++)//从小到大依次试
		{
			if (canPut(k, pos))
			{
				put(k, pos);
				go(pos + 1, k);//进入下一层
                //以下三行是撤销操作！
				arr[pos + k + 1] = 0;
				arr[pos] = 0;
				num[k] = 0;
			}
		}
}

int main()
{
	go(1,1);
}